ApproxMCv3: A modern approximate model counter
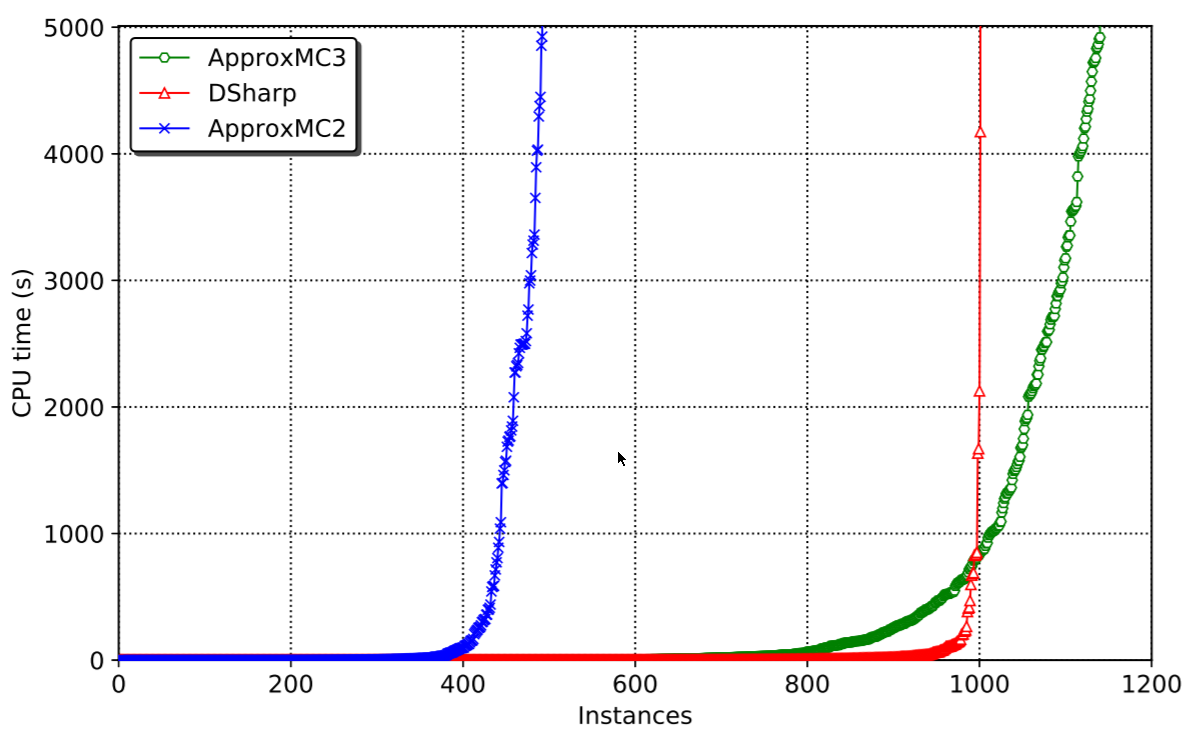
ApproxMC is a scalable, approximate model counter that provides PAC (probably approximately correct) guarantees. We have been working very hard on speeding up approximate model counting for SAT and have made real progress. The research paper, accepted at AAAI-19 is available here. The code is available here (release with static binary here). The main result is that we can solve a lot more problems than before. The speed of solving is orders(!) of magnitude faster than the previous best system:
Background
The idea of approximate model counting, originally by Chakraborty, Meel and Vardi was a huge hit back in 2013, and many papers have followed it, trying to improve its results. All of them were basically tied to CryptoMiniSat, the SAT solver that is maintained by Mate, as all of them relied on XOR constraints being added to the regular CNF of a typical SAT problem.
So it made sense to examine what CryptoMiniSat could do to improve the speed of approximate counting. This time interestingly coincided with the removal of XORs in CryptoMiniSat. The problem was the following: A lot of new in- and preprocessing systems were being invented, mostly by Armin Biere et al, and they couldn't be added to CryptoMiniSat, because they didn’t take into account XOR constraints. They handled CNF just fine, but not XORs. So XORs became a burden, and they were removed in versions 3 and 4 of CryptoMiniSat. But there was need, and this being an exciting area, the XORs had to come back.
Blast-Inprocess-Recover-Destroy
But how to both have and not have XOR constraints? Re-inventing all the algorithms for XORs was not a viable option. The solution we came up with was a rather trivial one: forget the XORs during inprocessing and recover them after. The CNF would always remain the source of truth. Extracting all the XORs after in- and preprocessing would allow us to run the Gauss-Jordan elimination on the XORs post-recovery.
The process is conceptually quite easy:
- Blast all XORs into clauses that are in the input using intermediate variables.
- Perform pre- or inprocessing.
- Recover the XORs from the CNF.
- Run the CDCL and Gauss-Jordan code at the same time.
- Destroy the XORs and goto 2.
This system allows for everything to be in CNF form, lifting the XORs out when necessary and then forgetting them when it’s convenient. All of these steps are rather trivial, except recovery, as explained below.
XOR recovery
Recovering XORs sounds like a trivial task. Let’s say we have the following clauses
x1 V x2 V x3 -x1 V -x2 V x3 x1 V -x2 V -x3 -x1 V x2 V -x3
This is conceptually equivalent to the XOR v1+v2+v3=1. So recovering this is trivial, and has been done before, by Heule in particular, in his PhD thesis. The issue with the above is the following: a stronger system than the above still implies the XOR, but doesn’t look the same. For example:
x1 V x2 V x3 -x1 V -x2 V x3 x1 V -x2 V -x3 -x1 V x2
This is almost equivalent to the previous set of clauses, but misses a literal from one of the clauses. It still implies the XOR of course. Now what? And what to do when missing literals mean that an entire clause can be missing? The algorithm to recover XORs in such cases is non-trivial. It’s non-trivial not only because of the complexity of how many combinations of missing literals and clauses there can be (it’s exponential) but because one must do this work extremely fast because SAT solvers are sensitive to time.
The algorithm that is in the paper explains all the bit-fiddling and cache-friendly data layout used along with some fun algorithms. We even managed to use compiler intrinsics to use target-specific assembly instructions for hamming weight calculation.
The results
The results, as shown above, speak for themselves. Problems that took thousands of seconds to solve can now be solved under 20. The reason for such incredible speedup is basically the following: CryptoMiniSatv2 was way too clunky and didn’t have all the fun stuff that CryptoMiniSatv5 has, plus the XOR handling was incorrect, loosing XORs and the like. The published algorithm solves the underlying issue and allows CNF pre- and inprocessing to happen independent of XORs, thus enabling CryptoMiniSatv5 to be used in all its glory. And CryptoMiniSatv5 is fast, as per the this year’s SAT Competition results.
We thank the National Supercomputing Center Singapore that allowed us to run a large number of benchmarks on their machines, using at least 200 thousand CPU hours to make this paper. This post has been adapted from Mate's post on ApproxMCv3.