WAPS: Weighted and Projected Sampling
This blogpost talks about our tool WAPS. Specifically, we will talk about how we are able to utilize the idea of sampling using knowledge compilations (d-DNNFs) from our previous work ( KUS) and generalize it in order to achieve weighted and projected sampling. You can read the paper here and get the tool here. You can read the previous blog that describes uniform sampling using knowledge compilations, though it is not absolutely necessary for this post.
Let’s talk about what it means to achieve weighted sampling at first.
Weighted Sampling
*** Given a formula $F$ and a weight function $W$, the objective of $weighted$ sampling is to draw samples from the set of satisfying assignments of $F$ called $R\_{F}$ using a generator $\mathcal{G}^{w}(F, W)$ that ensures $$\forall y \in R_{F}, \mathsf{Pr}\left[\mathcal{G}^{w}(F, W) = y\right] = \frac{W(y)}{W(R\_F)}$$Intuitively, this just means that the probability of drawing a sample is proportional to its weight. In our case, we are dealing with literal-weighted weight function and the weight of an assignment is simply given by the product of weight of individual literals in the assignment. Broadly speaking, WAPS proceeds in three stages:
- d-DNNF compilation
- Annotation
- Sampling.
Let’s look at what a typical d-DNNF looks like:
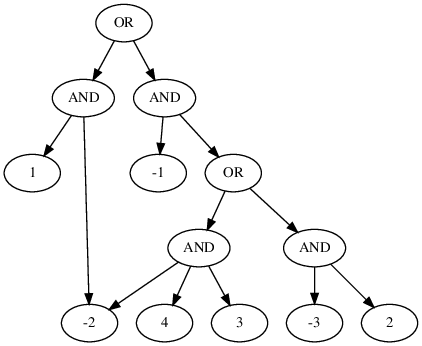
d-DNNF (Deterministic Decomposable Negation Normal Form) can be seen as a form of compact representation for the satisfying assignments of a given formula. One can also view it as the search space of component decomposition based DPLL procedures popularly employed in SAT solving and model counting. This perspective is helpful for Projected Sampling as you will see. Essentially, in a d-DNNF, the children of OR nodes have different (inconsistent to be precise) satisfying assignments (determinism); so, you can choose one of the children if you were to sample a satisfying assignment. On the other hand, the children of AND nodes are drawn over mutually disjoint sets of variables (decomposability); thus allowing you to simply stitch samples drawn from different children to get an overall sample.
WAPS proceeds by first compiling the given CNF formula into its d-DNNF. This is followed by Annotation. The central idea in WAPS is to annotate the compiled d-DNNF in a way which allows weighted sampling by simply performing weighted bernoulli trials over d-DNNF in the Sampling phase (Refer to our paper for more details). The weight annotation is summarised by the figures below:
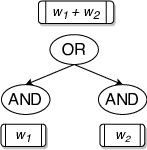
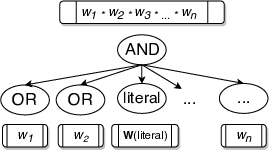
In our paper, we show that this annotation scheme allows you to perform weighted sampling.
Weighted and Projected Sampling
*** Given a formula $F$, a set of projecting variables $P$ and a weight function $W$, the objective of $weighted~and~projected$ sampling is to draw samples from the set of satisfying assignments of $F$ projected over $P$ called $R_{F\downarrow P}$ using a generator $\mathcal{G}^{wp}(F, P, W)$ that ensures $$\forall y \in R\_{F\downarrow P}, \mathsf{Pr}\left[\mathcal{G}^{wp}(F, P, W) = y\right] = \frac{W(y)}{W(R\_{F\downarrow P})}$$ Intuitively, this means that samples drawn contain only a subset of variables ($P$) as opposed to all variables in the formula and these samples obey the weight distribution given by $W$ over the variables appearing in samples. This has applications in hardware verification and other places where encoding original problem into CNF generates additional Tseitin variables while weight distribution is only defined on original variables in the problem. In such cases, we are often interested in samples from variables of the original problem.Projected Sampling
To achieve Projected Sampling, we aim to produce a d-DNNF which represents the set of satisfying assignments projected over a given set of projecting variables. To accomplish this, we modified Dsharp, a state of the art d-DNNF compiler to search first on projecting variables and then simply check if the residual formula is satisfiable to retain the corresponding path in d-DNNF. Notably, this technique has been used in the context of [Projected Model Counting](https://arxiv.org/abs/1507.07648) and [Quantitative Information Flow](https://link.springer.com/chapter/10.1007/978-3-642-40196-1_16) before.The above technique combined with weighted sampling sums up the buildup of WAPS (Weighted and Projected Sampler).