Barbarik

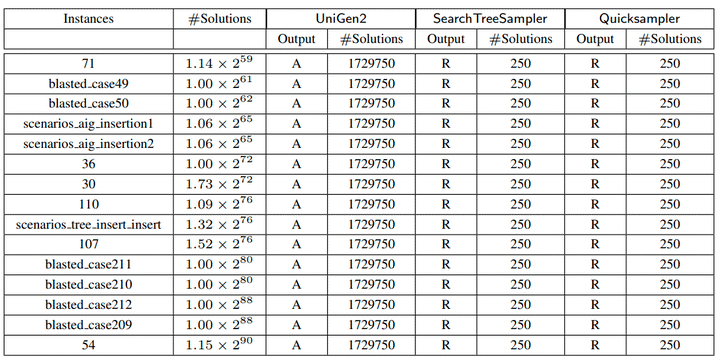
The divide between the existence of sampling techniques that have strong theoretical guarantees but fail to scale and scalable techniques with weak or no theoretical guarantees mirrors the gap in software engineering between poor scalability of classical program synthesis techniques and billions of programs that are routinely used by practitioners. One bridge connecting the two extremes in the context of software engineering has been program testing. In contrast to testing for deterministic programs, where one trace is sufficient to prove the existence of a bug, in case of samplers one sample is typically not sufficient to prove non-conformity of the sampler to the desired distribution. This makes one wonder whether it is possible to design testing methodology to test whether a sampler under test generates samples close to a given distribution.

We present, Barbarik, to test whether the distribution generated is ε−close or η−far from the uniform distribution. In contrast to the sampling techniques that require an exponential or sub-exponential number of samples for sampler whose support can be represented by n bits, Barbarik requires only O(1/(η − ε)4) samples.